接触角(ぬれ性)とは
接触角(ぬれ性)とは、表面の『水のはじき具合』を数値化したもので、液体がどれだけ表面に『なじんで広がるか』を表すため、塗料や接着剤のコーティング性能や洗浄度を、官能評価(見た目)ではなく定量化するための指標です。
よく洗浄された「清浄な」ガラス表面は、水によくぬれます。一方、フッ素コーティングなどで処理された表面は、水をはじきます。このような現象は日常しばしば経験しますが、この「ぬれ」の現象は、工学分野にて広く利用されています。
液体を固体表面に滴下すると、液体は自らの持つ「表面張力」で丸くなり、以下のような式が成り立ちます。
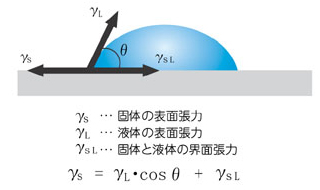
この式を「Youngの式」と言い、この液滴の接線と固体表面とのなす角度θを「接触角」(Contact Angle)といいます。「接触角」は「ぬれ」を表す指標としてはとても直感的でわかりやすく、あらゆる産業分野において、表面評価手法として採用されています。理化学辞典(岩波書店 第4版)においても「静止液体の自由表面が、固体壁に接する場所で、液面と固体面とのなす角(液の内部にある角をとる)」と記載されています。
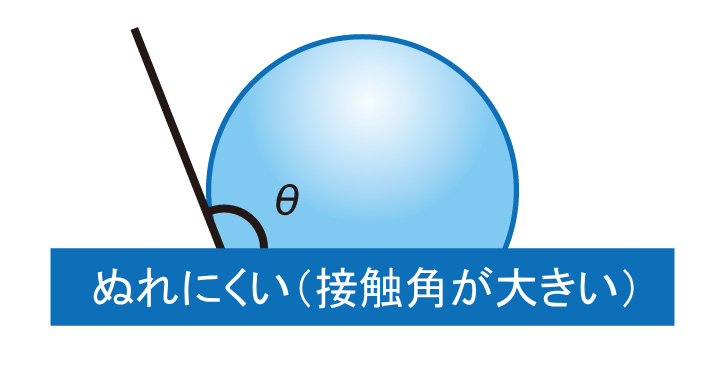
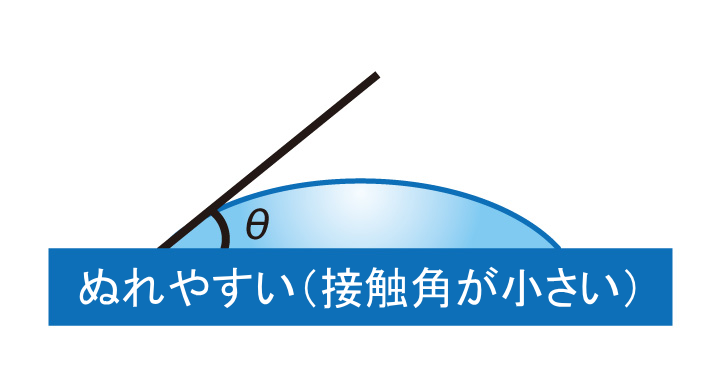
接触角の測定
θ/2法
-A half-angle Method -
接触角の測定は、一般的にθ/2法が用いられています。液滴の半径rと高さhを求め下式に代入して接触角を求めることができます。
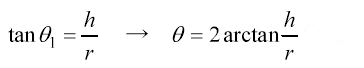
さらには、θ/2法は、液滴の左右端点と頂点を結ぶ直線の、固体表面に対する角度を求め、これを2倍することでも接触角を求められます。
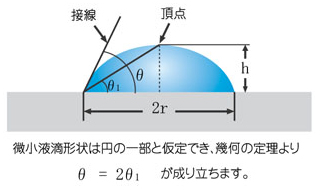
θ/2法は、液滴が球の一部であることを前提としているため、重力の影響を無視できる液滴量で測定します。分度器のような目盛があれば、直読でも測定ができます。パソコンによる解析でも、計算が簡単なのでごく短時間に処理できます。
接線法
-Tangent Method-
下図のように液滴端点近辺を球の一部とみなし、円弧上の点L1、L2、L3から円Oの中心Mを求め、点L1における円の接線を求めることができます。求めた円の接線と直線をなす角度が液滴左側の接触角となります。同様に円弧上の点R1、R2、R3から液滴右側の接触角を求めることができます。
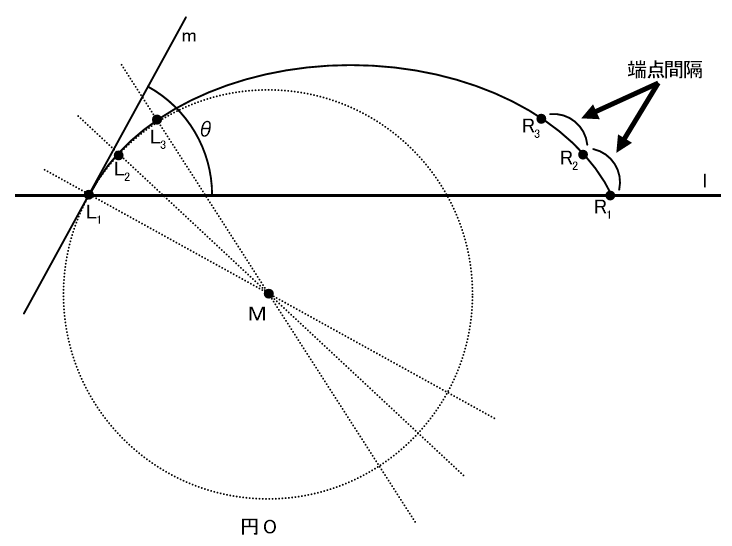
θ/2法は、取り込んだ液滴の幅と高さから接触角を計算しますので、求める接触角は左右の平均値となります。一方、接線法は、左右別に接触角を求めることができますので、固体表面の状態により、液滴左右の値にばらつきがある場合などは、より有効な測定法となります。
カーブフィッティング法
-Curve Fitting Method-
液滴の輪郭形状が真円または楕円の一部をなすと仮定し、指定された区間内(フィッティング区間)のすべての観測座標を使って最小二乗法フィッティングを行います。この計算により、真円または楕円のパラメータを決定し、端点における微分係数を求めて接触角を算出します。
接線法では、輪郭形状として真円が仮定されていますが、この結果と真円フィッティングの結果とを比較すると、真円フィッティングのほうがより多くの座標を利用していますので、ばらつきが小さくなります。実液滴では、重力の影響を受けて輪郭形状が潰れているため、真円からの逸脱が大きくなり、θ/2法や真円フィッティングでは、誤差が大きくなります。楕円フィッティングは、この誤差を低減するために用います。
しかし、真円フィッティングと比較すると、曲線を特徴づけるパラメータが1個多いので、計算結果としては不安定になります。
数学的には、楕円は真円を含みますが、実際には実験誤差を含むデータを使って解析しますので、統計学的には楕円フィッティングが万能というわけではありません。真円で十分に近似できるならば真円フィッティングを用いた方がより安定した結果が得られます。
このとき、ε値が近似の良否を判断する目安となります。理想的な状況、すなわち、画質が十分によく、かつ、近似も十分によいならば、ε=0.3dot程度です。ε値に完全に頼ることはできませんが、真円フィッティングと楕円フィッティングとを比較して、よりε値の小さな方を採用するのも一つの方法です。
動的接触角の測定
液滴が固体上で静止している状態の接触角は静的な接触角と表現されますが、液滴が固体上でぬれ広がる状態や液滴端点が動いていく状態の接触角測定は動的接触角と表現されます。
近年では、固体上の液滴の接触端点が動く「動的」な状況(前進接触角、後退接触角など)をシミュレーションソフトで評価するケースも増えています。
動的接触角の測定方法を下記に挙げます。
液滴法(経時変化)
-Sessile Drop Method in time function-
接触角測定を時間変化と共に連続的に行う測定です。固体表面へのぬれ性の変化、固体への吸収、液体の空気中への揮発の状況を解析します。
拡張/収縮法
-Extension/Contraction Method-
固体表面に接した液滴液量を大きくしたり、小さくしたりすることで、固体表面への液滴接触端点が前進、後退するときの接触角(前進接触角と後退接触角)を測定します。
【拡張】
【収縮】
拡張/収縮法は、固体表面における「乾燥状態からのぬれ広がり」(前進角)や「ぬれた状態からの液滴の除去」(後退角)の評価を行うものです。
滑落法(転落法)
-Sliding Method(Measurement on a slope)-
液滴を載せた固体試料を傾けて液滴を滑落させる方法です。装置全体を傾斜させることで、水平状態のみの測定では得られない、液体の固体に対する「滑りやすさ」「付着力」などのデータが得られます(下図)。
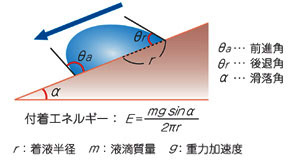
より詳しい理論はこちらをご覧下さい。
Wilhelmy法(プレート法、垂直板法)
-Wilhelmy method (plate method or vertical plate method)-
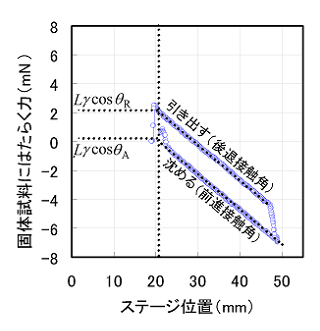
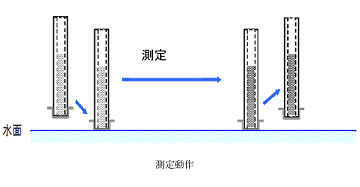
Wilhelmy法による動的接触角測定では、吊り下げた固体試料(プレート)を液体に「沈める時/引き上げる時」の力からそれぞれ「前進角/後退角」を算出しています。固体試料を液体試料に沈めるとき、固体試料はその周囲一周に液体との接触線を生じています。その一周の接触線において、液体の表面張力γLに接触線部分の固液接触角平均のθの余弦(cosθ)を乗じた力が固体試料に掛かっており、この力を電子天秤で測定し、計算によって前進角を求めています。計算には、固体試料が浸漬した分の浮力も考慮しております。また、後退角は固体試料を引き上げる際に同様の計算で求めています。
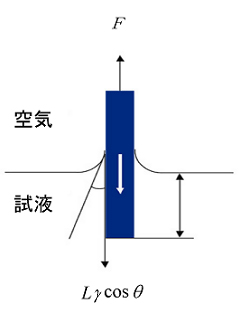

θ :固体試料と液体試料との接触角(表面張力測定の場合は0°が前提)
F :測定力(固体試料にはたらく力)
S :固体試料の断面積
h :固体試料の浸漬距離
ρ :液体試料の密度
g :重力加速度
L :固体試料の周囲長(既知でなければならない)
γ :表面張力(接触角測定の場合は既知でなければならない)
液面を上昇させると試料が浸漬し浮力が増加しますので、天秤に作用する力Fは小さくなります。また、液面を下降させると浮力が減少し、Fは大きくなります。このように液面を上昇、下降させたときの天秤に作用する力と液面の位置関係を表したのが右図です。
粉体接触角の測定
接触角は固体表面と液体とのぬれ性の評価指標です。粉体に対しても同様の考え方が成り立ち、接触角は粉体に対する液体のぬれ性を示します。 粉体の接触角測定には、ペレット状に圧縮成形した粉体の巨視的な表面に微小な液滴を滴下・着滴させ、着滴した液滴の輪郭形状を解析する方法や毛管現象を利用して接触角を求める方法などがあります。
浸透速度法
粉体への液体の浸透速度はLucas-Washburn式で表現されることが知られています。
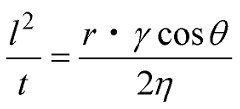
l…液体の浸透高さ
t…時間
r…充填粉体の毛管半径
γ…液体の表面張力
η…液体の粘度
θ…接触角
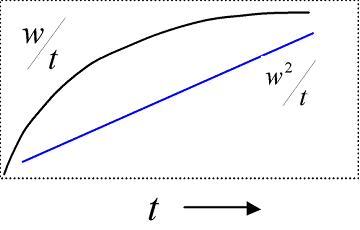
実際の測定では、粉体を充填したカラムに液体試料を浸透させ、経過時間tに対する重量Wの変化を追跡します。理想的にはW2に対してtをプロットすると直線的な関係が得られます。この直線の傾きから浸透速度や接触角を求めます。接触角を算出するためには、液体の表面張力や粘度のほか、充填粉体の毛管半径の値が必要です。毛管半径は、粉体に対して、十分にぬれのよい液体との接触角を0°とみなして実験的に決定します。

参考資料





